Relativitätstheorie relativ anschaulich

Sie packen die beiden vorher gebastelten dreidimensionalen Pappmodelle aus.
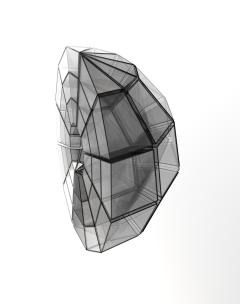
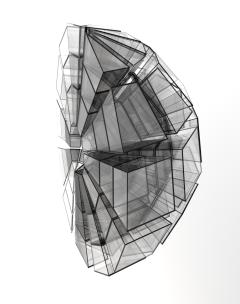
„Hier ist es genau das Gleiche! Das erste Modell, das in den hellen Farben, entspricht dem flachen Blatt. Es zeigt ein Stück ungekrümmten Raum, den Sie wie eine Torte in einzelne Sektoren zerlegt haben. Diese können Sie ohne Lücken hier im Restaurant wieder zusammensetzen, da der Raum hier ebenfalls (fast) nicht gekrümmt ist.
Das Modell in den dunklen Farben entspricht dem gekrümmten Blatt und zeigt ein Stück gekrümmten Raum. Stellen Sie sich eine riesige kugelförmige Torte um das Schwarze Loch herum vor. Sie wird genau wie ihr Gegenstück aus dem ungekrümmten Raum in einzelne Sektoren zerlegt und diese ergeben dann in verkleinertem Maßstab Ihre Pappkörperchen hier auf dem Tisch.
Genauso wenig wie die Stücke des gekrümmten Blattes auf einer ebenen Tischplatte zusammenpassen, passen die Stücke des gekrümmten Raums hier im ungekrümmten Restaurant zusammen! Maßstabsgerecht wieder vergrößert könnte man sie aber lückenlos um das Schwarze Loch herum anordnen.
Oder umgekehrt: Könnten wir ein maßstabsgerecht verkleinertes Schwarzes Loch hier ins Zentrum des Pappmodells setzen, würde es den Raum so krümmen, dass die Pappsektoren zusammenpassen würden. Dieses ‚Mini-Schwarze-Loch‘ müsste ungefähr die dreifache Masse der Erde haben. Das heißt, Sie müssten drei Planeten in Erdgröße auf die Größe einer Orange zusammenquetschen, um den Raum derart zu krümmen!
Jetzt sind wir in der Situation der Raupe und können uns nicht vorstellen, warum die Sektoren ums Schwarze Loch herum passen sollen und hier auf der Erde nicht. Wir können unseren Raum nicht von ‚außen‘ anschauen und sehen, wohin er sich krümmt.“
Das klingt einleuchtend. Sie spielen noch ein wenig mit dem gekrümmten Raum und kommen nochmals auf das Problem des größeren Rauminhalts zurück.
„Beide Modelle repräsentieren einen Ausschnitt aus dem Raum mit den gleichen Außenmaßen. Die gelben Außenflächen beider Modelle sind identisch. Man könnte annehmen, dass dann der Rauminhalt auch gleich sein muss.
Schauen Sie sich noch einmal die zwei Modelle der Blätter an. Beide haben den gleichen Umfang. Wie bei dem räumlichen Modell könnte man auf den gleichen Flächeninhalt schließen. Sie können aber deutlich sehen, dass das gekrümmte Blatt eine wesentlich größere Fläche hat.
Wenn Ihre Raupe wissen will, wie groß das Blatt ist, das sie zu verspeisen gedenkt, reicht es nicht, wenn sie einmal um das Blatt rumkrabbelt und den Umfang feststellt. Sie muss zusätzlich noch wissen, wie stark das Blatt gekrümmt ist.
Andersherum könnte sie die Krümmung des Blattes feststellen, indem sie zuerst den Umfang misst und dann die Fläche bestimmt, z. B. indem sie es auffrisst und sich dann auf die Waage stellt. Passen Sie auf Ihren Salat auf, die Raupe ist schon ziemlich weit!“
Ein verzweifelnder Kellner bringt Ihnen einen neuen Salat, Sie wollen die Studien der Raupe nicht stören.
„Genauso können wir, wenn wir den Raum um das Schwarze Loch vermessen, seine Krümmung feststellen! Stellen Sie sich das vor! Bisher konnten wir nur die kaum messbare Krümmung von Raum und Zeit in der Nähe der Sonne erforschen. Und jetzt haben wir ein richtiges Schwarzes Loch!“
Während sich Frau Panchakshari für die neuen Erkenntismöglichkeiten begeistert und ein etwas genervter Kellner die überall auf dem Boden herumliegenden Papierschnipsel zusammenfegt, denken Sie daran, dass es leider noch einige Jahrzehnte dauern wird, bis die Raumsonde ihr Ziel erreicht und das Schwarze Loch mit seiner enormen Krümmung von Raum und Zeit direkt erforscht.
Es wird noch viele interessante Mittagessen mit Frau P. geben und bei der nächsten Gelegenheit müssen Sie sie fragen, was es denn eigentlich mit der gekrümmten Zeit auf sich hat...
Kontakt: Möchten Sie uns eine Nachricht senden?