Relativitätstheorie relativ anschaulich
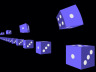
Der Gamovsche Radfahrer ist mit 93% der Lichtgeschwindigkeit unterwegs, wie man anhand der Längenkontraktion der Räder in Abb. 1 leicht berechnen kann. Das bedeutet für die Bewegung eines einzelnen Rads: Der Punkt auf dem Radmantel, der gerade die Straße berührt, ist in Ruhe, die Radnabe bewegt sich mit der Geschwindigkeit v=0,93c (c ist die Lichtgeschwindigkeit), und der Mantelpunkt oben auf dem Rad bewegt sich relativ zur Nabe mit 0,93c, relativ zur Straße also mit 2v/(1+v2/c2) = 0,997c gemäß der relativistischen Geschwindigkeitsaddition.
Wenn man ein Rad aus der Ruhe in eine Rotation mit annähernd Lichtgeschwindigkeit bringen möchte, stößt man allerdings auf ein gravierendes mechanisches Problem: Der Mantel wird, da er sich längs seines Umfangs bewegt, längenkontrahiert, bei einer Mantelgeschwindigkeit von v=0,93c um den Faktor γ=2,7. Die Speichen hingegen bewegen sich senkrecht zu ihrer Ausdehnung und werden somit nicht verkürzt.
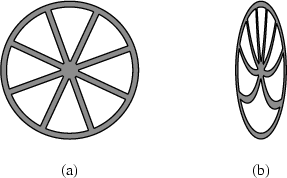
Ohne auf technische Details einzugehen, statten wir das relativistische Fahrrad deshalb mit Rädern aus, die in Rotation zusammengebaut werden. Dies geschieht so, dass sie stationär rotierend dieselbe geometrische Form haben wie übliche Räder in Ruhe (Abb. 11a).
Eine auf der Radfelge lebende Ameise würde dann allerdings einen Radumfang messen, der nicht das π -fache, sondern das 8.5-fache des Durchmessers beträgt: die innere Geometrie des so definierten Rades ist nicht euklidisch [ 9].
Kontakt: Möchten Sie uns eine Nachricht senden?