Film: Flug durch ein Wurmloch (kurz)
Der Film zeigt einen kurzen Flug durch das Wurmloch (Ausschnitt aus dem zweiten Film)
MPEG4 320×240 (1.1 MB), MPEG4 640×480 (6.9 MB)
Relativitätstheorie relativ anschaulich
Wurmlöcher sind durchquerbare Verbindungen zwischen zwei Universen oder zwischen zwei entfernten Regionen eines Universums. In Science-Fiction-Romanen werden sie daher gerne für Reisen zu außerirdischen Kulturen verwendet.
Die im folgenden beschriebenen Wurmlöcher sind exakte Lösungen der Einsteinschen Feldgleichungen; sie wurden von K. Thorne entwickelt, um dem Roman Contact von C. Sagan ([1]) eine wissenschaftliche Basis zu geben (Die Geschichte dieser Entwicklung ist in [2] erzählt; [3] erklärt den theoretischen Hintergrund).
Auch wenn diese Wurmlöcher von der Relativitätstheorie erlaubt werden, ergibt sich doch für die praktische Realisierung ein kleines Problem: Um die Raumzeit derart zu krümmen, dass sich ein Wurmloch bildet, wird eine exotische Materieform mit negativer Energiedichte benötigt. Für das hier beschriebene Wurmloch müsste der Betrag dieser Energiedichte extrem hoch sein, bis zum milliardenfachen der Dichte eines Neutronensterns. Ob es eine solche Materieform in unserem Universum gibt, ist nicht bekannt. Damit man durch das Wurmloch durchsehen und -fliegen kann, darf diese exotische Materie auch nicht mit unserer normalen Materie bzw. elektromagnetischer Strahlung wechselwirken.
Diese rein technischen Probleme können uns aber nicht davon abhalten, einen Flug durch ein solches Wurmloch im Computer zu simulieren.
Das hier gezeigte Wurmloch verbindet den Vorplatz vor den Gebäuden der physikalischen Institute der Universität Tübingen mit den schönen Sanddünen in der Nähe von Boulogne sur Mer im Norden Frankreichs (Bildquelle [4]) und wird von den MitarbeiterInnen der Theoretischen Astrophysik für kleinere Ausflüge in den Mittagspausen genutzt.
Um die Eigenschaften des gekrümmten Raums (der selbst unsichtbar ist) aufzuzeigen, ist hier um das Wurmloch herum ein aus 12 gelben Stäben bestehendes würfelförmiges Gitter aufgebaut. Die Stäbe selbst folgen Geodäten, d.h. geradmöglichsten Linien. Die sichtbaren Verzerrungen, insbesondere der Stäbe hinter dem Wurmloch, sind Folgen der Lichtablenkung im gekrümmten Raum.
Von den Ecken des gelben Würfels gehen acht grüne Stäbe radial nach innen. Sie laufen aufeinander zu und in einem ungekrümmten Raum müssten sie sich in der Mitte treffen. Im gekrümmten Raum des Wurmlochs tun sie das nicht.
Am Wurmlochschlund, der Grenzfläche zwischen den zwei durch das Wurmloch verbundenen Universen, treffen die Diagonalen auf die Ecken eines roten Würfels, dessen Kanten ebenfalls Geodäten sind. Die Diagonalen setzen sich geradlinig in das andere Universum fort, laufen dort wieder auseinander und treffen von innen auf die Ecken eines dritten Würfels (in Blau), der die gleichen Abmessungen hat wie der gelbe.
Die folgenden Filme zeigen einen Flug von Tübingen nach Boulogne sur Mer und zurück.
Das Wurmloch von außen
Das Wurmloch vor dem Physikgebäude der Universität Tübingen.
Wir nähern uns dem Schlund
Wenn wir uns dem Schlund nähern, wird der Blick auf die Landschaft auf der anderen Seite des Wurmlochs frei. Die grünen Diagonalen laufen geradlinig weiter.
Kurz vor dem Schlund
Hier ist zu sehen, dass die grünen Diagonalen von innen in die Ecken des blauen Würfels laufen.
Auf der anderen Seite
Beim Blick zurück erkennt man durch das Wurmloch hindurch die Gebäude der Universität in Tübingen.
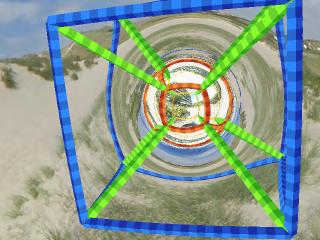
Das Wurmloch von außen
Hier sieht man das Wurmloch über der Düne in der Nähe von Boulogne sur Mer schweben.
Wir fliegen zurück
Rundflug am Schlund
Vor dem Durchqueren des Schlunds biegen wir nach oben ab und fliegen über die von dem roten Würfel gebildete Schlundebene. Die Diagonalen durchstoßen diese Ebene senkrecht.
Über der Schlundebene
Der rote Würfel erscheint als unendlich ausgedehnte Ebene. Die Ecken des Würfels sind flach und die quadratischen Seitenflächen haben Eckwinkel von 120 Grad. Solche, unserer Alltagsgeometrie widersprechenden "Würfel" gibt es nur in einem gekrümmten Raum.
Blick nach unten
Durch die Seitenflächen des roten Würfels können wir ins andere Universum blicken. Hier nach unten auf den Boden unterhalb des Wurmlochs in Tübingen.
Blick zur Seite
Schauen wir durch das nächste Quadrat, sehen wir zur Seite aus dem Wurmloch hinaus.
Blick nach oben
Wir fliegen ein Quadrat weiter. Hier schauen wir in den Himmel über dem Wurmloch.
Blick zur anderen Seite
Durch das nächste Quadrat blicken wir zur anderen Seite zu den Parkbänken. Diese stehen auf dem Kopf.
Noch ein Blick nach unten
Die Runde ist komplett. Wir sind einmal um das Wurmloch herum geflogen und schauen nochmal durch das erste rote Quadrat nach unten.
Zurück nach Tübingen
Wir fliegen wieder aus dem Wurmloch hinaus zurück nach Tübingen.
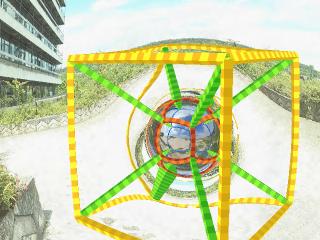
Das Wurmloch von außen
Dort schauen wir noch einmal zurück auf das Wurmloch.
Morris und Thorne ([3]) beschreiben ein Wurmloch als Lösung der Einsteinschen Feldgleichungen mit der Metrik:
\[ {\mathrm d} s^2 = {\mathrm d} l^2 + (b_0^2+l^2)\,({\mathrm d}\theta^2 + \sin^2 \theta \,{\mathrm d}\phi^2) \]
Der Wertebereich von \(l\) ist \( -\infty\ldots+\infty\). Die beiden Vorzeichen von \(l\) repräsentieren die beiden Universen, die für große \(|l|\) eine flache Minkowskigeometrie annehmen. Die Fläche \(l = 0\) (sphärische Topologie) verbindet die beiden Universen. Ihre Oberfläche wird durch den sogenannten Schlundradius \(b_0\) bestimmt.
In einer Orthonormalbasis \( (\hat{t}, \hat{l}, \hat{\theta}, \hat{\phi}) \) sind die einzigen nichtverschwindenden Komponenten des Riemanntensors
\[ R_{\hat{\theta}\hat{\phi}\hat{\theta}\hat{\phi}} = -R_{\hat{l}\hat{\theta}\hat{l}\hat{\theta}} = -R_{\hat{l}\hat{\phi}\hat{l}\hat{\phi}} = b_0^2 / (b_0^2 + l^2)^2 \]
sowie die aus Symmetrien folgenden Komponenten. Durch Einsetzen der Metrik in die Feldgleichungen erhalten wir den Energieimpulstensor:
\[ -T^{\hat{t}\hat{t}} = -T^{\hat{l}\hat{l}} = T^{\hat{\theta}\hat{\theta}} = T^{\hat{\phi}\hat{\phi}} = 8{\mathrm \pi} \,b_0^2 / (b_0^2 + l^2)^2. \]
Er hat die unangenehme Eigenschaft, dass die Energiedichte \( T^{\hat{t}\hat{t}} \) negativ ist, was eine technische Realisierbarkeit bzw. ein natürliches Vorkommen nach heutigem Stand der Wissenschaft ausschließt.
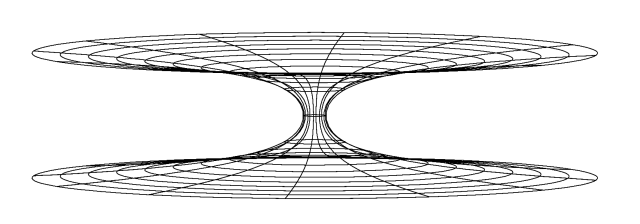
Aufgrund der sphärischen Symmetrie kann man die wesentlichen Eigenschaften der Metrik sowie den Verlauf von Lichtstrahlen beschreiben, wenn man eine zweidimensionale Ebene durch den Ursprung betrachtet und diese in einen dreidimensionalen euklidischen Raum einbettet. Die räumliche Metrik in der Äquatorebene lautet:
\[ {\mathrm d} s^2 = {\mathrm d} l^2 + (b_0^2+l^2) {\mathrm d}\phi^2. \]
Mit
\[ r=\sqrt{b_0^2+l^2} \]
besteht die Einbettungsfläche (obiges Bild) aus den Punkten mit den kartesischen Koordinaten \(x\), \(y\) und \(z\):
\[ \begin{align*} x &= r\, \cos\phi \\\ y &= r\, \sin\phi \\\ z &= b_0\, \log\left[\frac{r}{b_0} + \sqrt{\left(\frac{r}{b_0}\right)^2 - 1}\right] \cdot \left\{ \begin{array}{rl} -1 & l\lt 0 \\ 0 & l=0 \\ +1 & l \gt 0. \end{array} \right. \end{align*} \]
[1] C. Sagan, Contact, Simon and Schuster, 1985.
[2] K. Thorne, Gekrümmter Raum und verbogene Zeit, Knaur, München, 1994.
[3] M. S. Morris, K. S. Thorne, Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity, Am. J. Phys. 56, 395-412, 1988.
[4]
Philippe E. Hurbain
,
Panoramaaufnahme von Sanddünen in der Nähe von Boulogne sur Mer
im Norden Frankreichs.
Kontakt: Möchten Sie uns eine Nachricht senden?