Relativitätstheorie relativ anschaulich

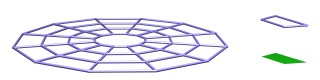




Aus dem Vergleich der beiden Klötzchenmodelle in den Abbildungen 2 und 3 ergeben sich einige direkte Folgerungen zur Geometrie in der Nähe eines Schwarzen Lochs.
Um solche Vergleiche zu erleichtern sind die Modelle nach demselben Schema gebaut und außerdem gleich groß. Dabei ist "gleich groß" in folgendem Sinn zu verstehen: Von außen gesehen sind die Modelle Kugeln und beide haben dieselbe Außenfläche. Innen ist jeweils eine Kugel herausgeschnitten; auch die Innenkugel hat in beiden Modellen dieselbe Oberfläche. Durch Aneinanderhalten der Klötzchen kann man sich von beidem leicht überzeugen.
Volumen. Beide Modelle beschreiben eine dickwandige Hohlkugel und haben gleich große Begrenzungsflächen innen und außen. Sie unterscheiden sich aber dadurch, dass die Klötzchen in radialer Richtung länger sind, wenn ein Schwarzes Loch im Zentrum sitzt als wenn das Zentrum leer ist. Das kann man am besten durch Aneinanderhalten der Klötzchen sehen; es ist aber auch in den Abbildungen 2 und 3, die denselben Maßstab haben, deutlich zu erkennen.
Wenn also ein Schwarzes Loch im Zentrum der Hohlkugel sitzt, dann hat jedes einzelne Klötzchen ein größeres Volumen als das entsprechende Klötzchen des Modells mit einem leeren Zentrum. D. h. zwischen dieselben Begrenzungsflächen passt mehr Volumen. Oder mit anderen Worten: der Zusammenhang zwischen Volumen und Oberfläche einer Kugel ist im gekrümmten Raum anders als wir es vom (nahezu) ungekrümmten, euklidischen Raum auf der Erde her kennen.
Hier kann man noch einmal an die zweidimensionale Analogie und die Flächenwesen zurückdenken: Ein Kreis in der Ebene und ein Kreis um eine Hügelkuppe umschließen beim selben Umfang verschieden große Flächen.
Umfang. Wir betrachten zwei Kreise um das Zentrum, die auf der äußeren bzw. inneren Begrenzungsfläche liegen. Abmessen zeigt: Im leeren Raum ist das Verhältnis aus der Differenz der Umfänge zur Differenz der Radien 2π, wie erwartet.2Befindet sich aber ein Schwarzes Loch im Zentrum, dann ist dieses Verhältnis kleiner! Die beiden Kreisbahnen sind weiter voneinander entfernt, als man aufgrund der Bahnlängen erwarten würde. (Hier werden nur die Differenzen der Radien bestimmt, weil die Radien selber nicht abgemessen werden können. Das Modell des Schwarzen Lochs reicht nicht bis ins Zentrum und kann auch nicht bis dorthin fortgesetzt werden.)
Beim Abmessen der Bahnlängen taucht unter Umständen die Frage auf, wie man mit den Lücken zwischen den Klötzchen umgehen soll. Das wird klar, wenn man sich noch einmal die Konstruktion des Modells vor Augen hält: Die Gitterzellen füllen den gekrümmten Raum lückenlos aus. Die nachgebauten Klötzchen passen nur deshalb nicht lückenlos zusammen, weil man sie in einem ungekrümmten Raum zusammenzusetzen versucht. Man muss also die Seiten, welche die Gitterzellen gemeinsam haben, auch bei den Klötzchen identifizieren. Wenn man eine Bahn über mehrere Klötzchen hinweg verfolgen will, dann muss man sich von Klötzchen zu Klötzchen hangeln: Immer wenn man an einen Rand gelangt, wird das Nachbarklötzchen angelegt und man macht so weiter, als wären die beiden Teile eine Einheit.
An den Umfängen und Radiusdifferenzen kann man auch erkennen, dass der Raum nicht überall gleich stark gekrümmt ist. Das Modell besteht ja aus drei konzentrischen Schichten von Klötzchen. Wenn man für jede Schicht einzeln die Umfänge außen und innen sowie die Schichtdicke bestimmt, stellt man fest, dass das Verhältnis aus Umfangdifferenz zu Radiendifferenz für die innerste Schicht am kleinsten ist und nach außen ansteigt - weiter weg vom Schwarzen Loch ist der Raum also weniger stark gekrümmt.
Geraden. "Zwei Punkte legen eine Gerade fest" lernt man in der Geometrie. Gilt das auch in der Nähe eines Schwarzen Lochs? Um die Frage zu beantworten, konstruieren wir gerade Linien.
Dafür und ebenso für die Anwendungen im folgenden Abschnitt ist allerdings das dreidimensionale Modell zu unhandlich. Wir beschränken uns deshalb auf einen zweidimensionalen Ausschnitt. Er liegt in einer Äquatorebene des Schwarzen Lochs: Abbildung 7 zeigt den entsprechenden Ausschnitt des Gittergerüsts. Er ergibt im Klötzchenmodell von Abbildung 3 die annähernd horizontalen grünen Seitenflächen. Diese Seitenflächen sind eine zweidimensionale Karte für einen Ausschnitt aus der Äquatorebene (Abb. 8). Mit den Flächenstücken, die leicht in größerer Anzahl zugeschnitten werden können (Kopiervorlagen zum Selbstausdrucken stehen unter [ 2] zur Verfügung), können die weiteren "Experimente" nachvollzogen werden.
Auf der zweidimensionalen Karte konstruieren wir nun gerade Linien3. Wie eine gerade Linie verläuft, ist innerhalb eines Flächenstücks klar, aber was ist zu tun, wenn man an den Rand gelangt? Hier gilt dasselbe, was bereits oben über die Lücken gesagt wurde: Die Ränder von zwei benachbarten Kartenstücken stellen ein und denselben Gitterstab dar (Abb. 7), sind also identisch. Beim Einzeichnen einer Linie hangelt man sich daher von Stück zu Stück, indem man immer das benötigte Nachbarstück anlegt und die Linie dann gerade weiterführt, so als hätte man die beiden Teile nie auseinandergeschnitten.
Eine gerade Linie, die quer durch die Karte verläuft (untere Linie), zeigt Abbildung 9. Oben ist eine weitere Linie eingetragen, welche dieselben Endpunkte verbindet. Umlegen der Stücke zeigt, dass auch die zweite Linie gerade ist (Abb. 10). Abbildung 11 zeigt beide Linien bei einer symmetrischen Anordnung der Kartenstücke. Die Aussage, dass zwei Punkte genau eine Gerade festlegen, gilt offensichtlich nicht in der Umgebung eines Schwarzen Lochs.
Die hier konstruierten geraden Linien sind Beispiele für Geodäten: Linien in einem beliebig gekrümmten Raum, die an jedem Punkt lokal gerade verlaufen.
Kontakt: Möchten Sie uns eine Nachricht senden?