Relativitätstheorie relativ anschaulich





Das Modell stellt die Umgebung eines Schwarzen Lochs dar und ermöglicht es, dort "Messungen durchzuführen". Zum Vergleich dient ein zweites Modell, das einen Raumbereich weit weg von allen Massen darstellt. Ein Gedankenexperiment beschreibt, wie die beiden Modelle konstruiert werden:
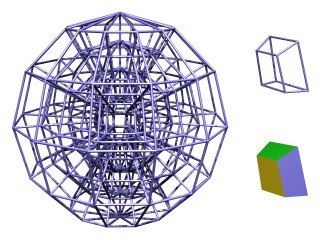
Wir errichten ein Gerüst in dem leeren Raum um das Schwarze Loch bzw. in einem leeren Raum weit weg von allen Massen (Abb. 1 links). Wir messen die Längen aller Gitterstäbe, bauen die Gitterzellen verkleinert als Klötzchen nach (Abb. 1 rechts) und setzen sie zusammen.
Abbildung 2 zeigt das Vergleichsmodell, Abbildung 3 das Modell für die Umgebung des Schwarzen Lochs. Der vermessene und aus Klötzchen nachgebaute Raumbereich ist von außen gesehen eine Kugel. Innen ist er hohl; im Zentrum wird eine kleine Kugel ausgespart, die etwas größer als der Ereignishorizont des Schwarzen Lochs ist 1.
Beginnen wir mit dem Modell ohne Schwarzes Loch (Abb. 2). In der Computergrafik ist etwas mehr als die Hälfte der Klötzchen abgebildet. Man erkennt die ausgesparte Innenkugel; sie ist von drei Schichten Klötzchen umgeben, die wie Zwiebelschalen ineinander liegen.
Ein solches Klötzchenmodell kann man wie eine Landkarte in drei Dimensionen verwenden: Man kann Orte darauf markieren, Routen einzeichnen und Entfernungen messen.
Wie sich die Anwesenheit eines Schwarzen Lochs auf den Raum in seiner Umgebung auswirkt, zeigt das zweite Modell (Abb. 3): Auch hier wurde eine Hohlkugel vermessen. Wenn man aber versucht, die Klötzchen zusammenzusetzen, kommt dabei keine Hohlkugel heraus. Die Bauteile "passen nicht", sie fügen sich nicht zu einem Ganzen. In der Abbildung sind die Klötzchen symmetrisch angeordnet; man erkennt an den Lücken, dass man sie nicht zu einer Hohlkugel zusammenschieben kann. Diese Eigenschaften des Klötzchenmodells zeigen an, dass der Raum um das Schwarze Loch eine innere Krümmung hat. Auch hier ist das Klötzchenmodell eine Karte. Und die Karte verrät eine Menge über den gekrümmten Raum.
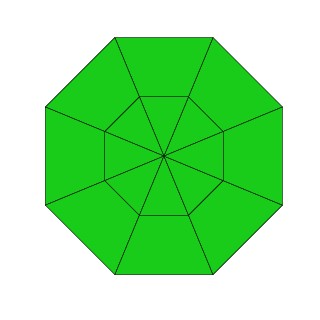
Um zunächst einmal einzusehen, dass das Auftreten solcher Lücken genau das ist, was man bei einem gekrümmten Raum zu erwarten hat, verlagern wir die ganze Überlegung von drei in zwei Dimensionen: Eine Fläche wird mit einem Gitter überzogen, dieses ausgemessen, die Flächenstücke nachgebaut und auf dem Tisch ausgelegt. Wenn die Fläche eben ist (Abb. 4), dann passen die Stücke lückenlos aneinander. Wenn die Fläche aber wie ein Hügel gewölbt ist (Abb. 5), bleiben Lücken.
Um die Analogie komplett zu machen, müssen wir zusätzlich noch unseren Standpunkt wechseln. Wir können uns drei Raumdimensionen vorstellen. Damit ist uns klar, wie sich eine hügelförmige Fläche in die dritte Dimension krümmt und dass man diese Fläche aufschneiden muss um sie in der Ebene auszubreiten. Bei einem Raumstück dagegen können wir uns nicht vorstellen, dass es sich in irgendwelche höheren Dimensionen krümmt und dass man es aufschneiden muss, um es in unseren ungekrümmten Raum hineinzusetzen. Edwin A. Abbott beschrieb im vorletzten Jahrhundert in seinem Roman "Flächenland" die Weltsicht von Flächenwesen, die in einer zweidimensionalen Fläche leben und sich nur zwei Dimensionen vorstellen können ([ 3]). Wenn ein solches Flächenwesen die Oberfläche eines Hügels vermisst, dann kann es sich auch auf dem Hügel nur vor, zurück, nach rechts oder nach links bewegen. Die Richtungen oben und unten gibt es innerhalb der Fläche nicht, egal ob sie nun eben ist oder gekrümmt. Aber an den ausgemessenen Flächenstücken kann ein Flächenwesen klar erkennen, wo seine Welt gekrümmt ist und wo nicht. Genau so ergeht es uns "Raumwesen", wenn wir unsere dreidimensionale Welt vermessen.
Würde man die Flächenstücke von Abbildung 5 auf einem maßstabsgerecht verkleinerten Hügel anordnen, dann würden sie so wie sie sind lückenlos zusammenpassen. Dasselbe gilt für die Klötzchen von Abbildung 3: Könnten wir ein maßstabsgerecht verkleinertes Schwarzes Loch in das Zentrum des Modells setzen, dann würden die Klötzchen in dem jetzt gekrümmten Raum so wie sie sind lückenlos zusammenpassen.
Um sich mit der Idee vertraut zu machen, dass die Flächenstücke bzw. die Klötzchen eine Karte darstellen, kann man dieselbe Überlegung auf die Erdoberfläche anwenden. Wenn man ein Gitter aus Längengraden und Breitenkreisen mit Abständen von jeweils 30° wählt und die zugehörigen Flächenstücke erstellt, erhält man die Karte von Abbildung 6. Zusammengenommen decken die Stücke die gesamte Erdoberfläche ab. Im Gegensatz zu üblichen Weltkarten erhält man so kein geschlossenes Kartenbild. Das ist sicher ein Nachteil dieser Karte, mit dem man sich aber andererseits einen Vorteil erkauft: Die gestückelte Karte ist überall maßstabsgestreu und verzerrungsfrei; keine Projektion mit geschlossenem Kartenbild kann das erreichen.
Das Beispiel zeigt auch deutlich, welche Näherung in der gestückelten Karte steckt: Hier wird die Oberfläche eines Globus durch eine Anzahl ebener Flächenelemente angenähert. Die Näherung ist offensichtlich umso besser, je kleiner die Flächenelemente sind. Dieselbe Näherung steckt in der Klötzchenkarte: Der gekrümmte Raum wird durch eine Anzahl von Raumelementen angenähert, von denen jedes einzelne ungekrümmt (euklidisch) ist. Auch diese Näherung ist umso besser, je kleiner die einzelnen Elemente sind.
Die Darstellung eines gekrümmten Raums durch (euklidische) Klötzchen basiert auf dem Prinzip des Regge-Calculus ([ 4]), bei dem die vierdimensionale Raum-Zeit in kleine Elemente eingeteilt wird, deren innere Geometrie jeweils flach ist. Typische Anwendungen des Regge-Calculus liegen in den Bereichen numerische Relativitätstheorie und Quantengravitation. Mit dieser Arbeit möchten wir zeigen, dass der Ansatz auch für die didaktische Aufbereitung der Allgemeinen Relativitätstheorie sehr fruchtbar ist. Sein großer Vorteil besteht darin, dass er eine koordinatenfreie Darstellung der Raumzeit liefert, so dass durchweg mit Beobachtungsgrößen argumentiert werden kann.
Die beiden Klötzchenmodelle können mit den oben bereits erwähnten Bastelbögen aus Pappe nachgebaut werden. Dabei ist es nicht notwendig, die vollständigen Modelle aus je 216 Klötzchen zu bauen. Da dies nur die zähesten Modellbauer wirklich erfreuen würde, haben wir die Aufteilung (die ja völlig willkürlich ist) so symmetrisch gewählt, dass 9 Klötzchen je Modell bereits die ganze Information enthalten.
Im folgenden beschreiben wir, wie man durch "Experimente" mit dem Klötzchenmodell Geometrie und Physik in der Nähe eines Schwarzen Lochs untersuchen kann.
Kontakt: Möchten Sie uns eine Nachricht senden?