Der gekrümmte Raum

Sehr geehrte/r ...,

die Raumkarte für das Schwarze Loch ist eine sehr gute Idee. Ich stimme Ihnen zu, dass die Kugel ein Blickfang im Kontrollraum sein wird!

Allerdings müssen Sie unbedingt berücksichtigen, dass der Raum in der Nähe des Horizonts stark gekrümmt ist!

In diesem Schwarzen Loch ist die Masse von zehn Sonnen in einem Gebiet von der Größe einer Stadt enthalten. In seiner unmittelbaren Umgebung ist der Raum deshalb stark gekrümmt. Stellen Sie sich vor, Sie wären ganz in der Nähe von IBH 1645+45 und würden die Sektoren Ihrer Raumkarte Kante für Kante und Winkel für Winkel vermessen. Ich habe für Sie berechnet, welche Sektorformen Sie finden müssten und schicke Ihnen anbei Vorlagen für ein physikalisch korrektes Modell eines Schwarzen Lochs ².

Als weitere Anlage füge ich die Messvorschrift für die Sektorvermessung bei (als Gedankenexperiment formuliert). Ich erscheine ungern pedantisch, aber die genaue Beschreibung von Messungen bis hin zu scheinbar unwichtigen Details ist nunmal das A und O in der Relativitätstheorie.

Beste Grüße,

Deepta Panchakshari

Anlagen

Bauanleitung:

1. Tipps: Die Pappe lässt sich gut knicken, wenn man die Knicklinien vorher leicht einritzt. Für die Klebestellen eignet sich am besten flüssiger Alleskleber. Lösemittelfreier Kleber und Klebestifte haben sich nicht bewährt.
2. Die Bauteile von Puzzle 2 werden ausgeschnitten, an den schwarzen Strichen gefalzt und mit Hilfe der weißen Klebelaschen zu Hohlkörperchen zusammengeklebt.
3. Legen Sie die Hohlkörperchen so nebeneinander, dass gelbe und grüne Flächen gleicher Farbe, Größe und Form aneinanderstoßen.

Anlage D. P., 15.3.2012

Messvorschrift für die Sektoren (Gedankenexperiment!)

1. In dem zu vermessenden Raum wird ein Gittergerüst errichtet.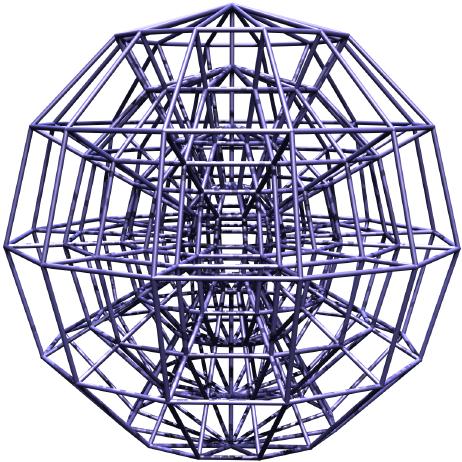

2. Als Experimentatoren bewegen wir uns durch das Gitter und messen die Längen der Gitterstäbe sowie die Winkel zwischen ihnen. Damit kennen wir die Form und die Größe jeder Gitterzelle. 3. Wir bauen die Gitterzellen verkleinert aus Pappe nach.

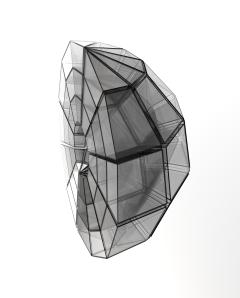
Wenn das Gitter im leeren Raum steht, weit weg von jeder Masse, dann sehen die Gitterzellen so aus wie in Ihrem Modell.

Für mein Modell habe ich mitten in dasselbe Gitter ein Schwarzes Loch mit zehn Sonnenmassen gesetzt. Mit demselben Gitter meine ich, dass das Gitter nach demselben Schema gebaut und außerdem gleich groß ist. Wobei gleich groß (noch ein wenig Geduld, bitte!), sorgfältig definiert, die folgende Bedeutung hat:

Ihr Pappmodell füllt eine Kugel mit einer Oberfläche von 2700 Quadratzentimetern aus. Wenn man die äußerste Lage Gitterzellen entfernt, bleibt eine Kugel von 1500 Quadratzentimetern Oberfläche. Entfernt man auch die zweite Lage, dann hat die verbleibende Kugel 700 Quadratzentimeter Oberfläche. Die dritte und innerste Lage von Gitterzellen umschließt einen kugelförmigen Hohlraum mit 200 Quadratzentimetern Oberfläche.

In meinem Pappmodell sind diese vier Kugeloberflächen gleich groß wie in Ihrem.

Liebe Frau Panchakshari,

das Modell ist fertig! Wir haben auch schon heftig darüber diskutiert. Aber, um ganz ehrlich zu sein, so richtig haben wir den gekrümmten Raum noch nicht verstanden, den wir da gebaut haben. Für uns Planetenforscher sind Schwarze Löcher schon sehr exotische Objekte. Und was die Allgemeine Relativitätstheorie angeht, die ja als eine der schwierigsten Theorien überhaupt gilt, müssen Sie verstehen, dass wir allesamt keine Theoretiker sind, sondern Praktiker, die sich normalerweise mit Raketentechnik, Instrumentenbau und Datenauswertung beschäftigen. Vielleicht könnten Sie uns mit einer anschaulichen Erklärung weiterhelfen?

Ich fasse unsere Diskussion kurz zusammen:

Die beiden Raumfahrttechniker in unserem Team haben sofort erklärt, dass Ihr Modell nicht richtig sein kann (jedenfalls nicht so, wie wir es gebaut haben), weil aus solchen Pappkörperchen niemals eine komplette Kugel wird.

Für unser erstes Modell, das in den hellen Farben, haben wir aus den neun Pappkörperchen einen Schnitz gebaut, der wie ein Stück Schokobombe aussieht. D. h. mehrere Schnitze könnten wir wie Kuchenstücke zu einer Halbkugel zusammenschieben.

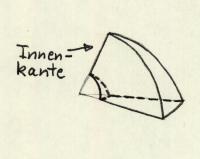
Für Ihr Modell, das in den dunklen Farben, haben wir ebenfalls die Pappkörperchen zu einem Schnitz zusammengesetzt. Aber bei diesem Schnitz steht die Innenkante nicht senkrecht auf dem Boden! Solche Kuchenstücke ergeben keine Halbkugel. Zuerst dachten wir, sie ergäben stattdessen einen Gugelhupf. Aber es ist noch schlimmer: Zwischen benachbarten „Kuchenstücken“ bleiben beim Zusammenschieben Lücken.

Unser Feinmechaniker ist außerdem der Meinung, dass beim zweiten Modell bereits die Pappkörperchen nicht richtig zu einem Schnitz zusammenpassen. Tatsächlich bleiben immer kleine Ritzen und Lücken, egal wie wir auch schieben. Die Bauingenieurin hält dagegen, dass die Ritzen doch wirklich klein sind und meint, wir hätten einfach nicht sorgfältig genug ausgeschnitten. Über diesen Punkt konnten wir uns nicht einigen, denn solange man nur zwei Pappkörperchen aneinanderhält, ist seltsamerweise nie ein Fehler zu erkennen, die Flächen passen immer hervorragend zusammen.

Unser zweiter Streitpunkt ist der Rauminhalt des Modells – er ist nämlich zu groß! Wir haben an den Modellen Ihre Messvorschrift überprüft: Die gelben Außenflächen der Sektoren (der Pappkörperchen) sind in der Tat bei beiden Modellen gleich groß. Also haben die beiden Kugeln dieselbe Oberfläche. Dasselbe gilt für die gelben Innenflächen, d. h. auch der ausgesparte Hohlraum hat bei beiden Modellen dieselbe Oberfläche. Dann ist uns aber aufgefallen, dass die blauen und grünen Seitenflächen im zweiten Modell größer sind als im ersten. Folglich hat jeder einzelne Sektor einen größeren Rauminhalt als der entsprechende Sektor im ersten Modell, und dasselbe gilt für das komplette Modell aus allen Sektoren. Wir haben hier zwei Kugeln mit gleich großen Oberflächen, aber verschiedenem Rauminhalt. Oder anders gesagt: Die zweite Kugel ist innen größer als außen.

Der Leiter unseres Rechenzentrums, der von Hause aus Mathematiker ist, sieht darin kein Problem; er sagte etwas von nichteuklidischer Geometrie und dass sich Mathematiker mit solchen Ideen schon länger beschäftigen. Er hat auch versucht, uns die Sache zu erklären, aber das übersteigt mein Vorstellungsvermögen: Wie soll ich denn bitte verstehen, dass in einer Kugeloberfläche nicht das zugehörige Kugelvolumen drin ist, sondern mehr? Unser Architekt hat sich übrigens bestens amüsiert; er wirbt, wie er sagt, gerne damit, dass seine Häuser innen größer sind als außen, hat aber noch nie gedacht, dass das jemand ernst nehmen könnte.

Ich finde Ihr Modell des gekrümmten Raums hochinteressant und möchte es unbedingt für das Kontrollzentrum bauen lassen, aber ich habe noch Überzeugungsarbeit zu leisten. Die Leute aus der Informatikabteilung meinen, man sollte doch einfach bei dem ersten Modell bleiben, das jeder versteht und das genauso schön aussieht. Und meine Leiterin der Abteilung Öffentlichkeitsarbeit rauft sich die Haare bei dem Gedanken, dass sie den Journalisten erklären muss, was sie da genau vor sich haben...

Für Ihre weitere Unterstützung wäre ich sehr dankbar. Vielleicht könnten wir uns gelegentlich zum Mittagessen treffen?

Beste Grüße