Relativitätstheorie relativ anschaulich

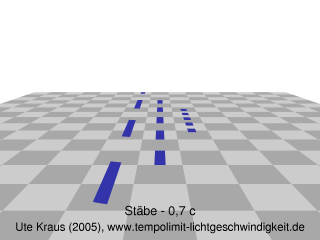
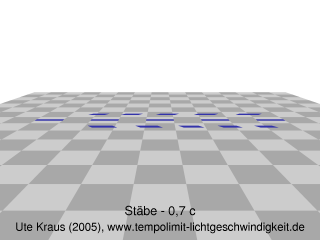
Einmal angenommen, wir würden über Raumschiffe verfügen, die annähernd Lichtgeschwindigkeit erreichen können - würden sie dann im Flug gestaucht aussehen, je schneller, desto kürzer? Nun, ganz so einfach ist es nicht, wie erstmals von Anton Lampa im Jahr 1924 gezeigt wurde [ 1]. Eine Computersimulation zeigt, was Lampa berechnete (Abb. 1): Maßstäbe, die sich fast lichtschnell nähern (links, 70% der Lichtgeschwindigkeit), sehen wesentlich länger aus als Maßstäbe, die sich mit der gleichen Geschwindigkeit entfernen (rechts). Ja, sie scheinen sogar länger zu sein als ruhende Maßstäbe (Mitte). Dabei sind alle diese Maßstäbe, wenn sie ruhend abgemessen werden, gleich lang. Sie haben dann genau die Länge eines der Karos auf dem Untergrund. In Abb. 2 blicken wir von der Seite auf dieselbe Szene. Alle bewegten Stäbe erscheinen verkürzt!
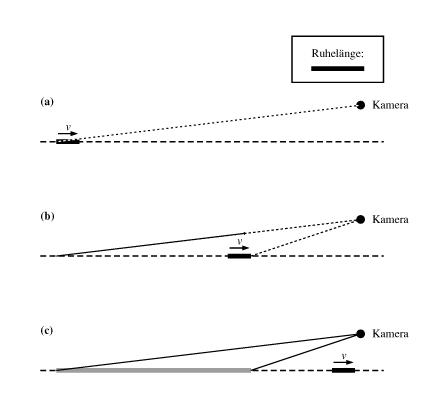
Um das Aussehen der bewegten Maßstäbe zu verstehen, muss man sich bewusst machen, wie das gesehene (oder photographierte) Bild entsteht. Das Bild eines Objekts entsteht dadurch, dass Licht vom Objekt ausgehend in die Kamera gelangt. Dabei legt das Licht den Weg zwischen Objekt und Kamera mit einer zwar sehr großen, aber doch endlichen Geschwindigkeit zurück. Da verschiedene Objektpunkte verschieden weit von der Kamera entfernt sind, ist das Licht je nach Ursprungsort verschieden lange unterwegs.
Wird die Kamera ausgelöst, dann registriert sie das Licht, das zu diesem Zeitpunkt gerade ankommt. Das gleichzeitig eintreffende Licht wurde aber, je nach Laufzeit, innerhalb eines gewissen Zeitraums nach und nach emittiert. Während dieses Zeitraums bewegte sich nun das Objekt ständig weiter. Abb. 3 illustriert am Beispiel eines einzelnen heranfliegenden Stabs, was das zur Folge hat: Das Licht, das zu einem Zeitpunkt in die Kamera eintritt, stammt von Punkten im Raum, die sich über mehr als eine Stablänge erstrecken; der Stab erscheint verlängert. Dieser Lichtlaufzeiteffekt ist so groß, dass er sogar die Längenkontraktion überwiegt.
Wenn sich umgekehrt der Stab von der Kamera entfernt, führt der Lichtlaufzeiteffekt zu einer scheinbaren Verkürzung, die zur Längenkontraktion noch hinzukommt: Der Stab erscheint stark verkürzt.
Nur in dem einen Fall, in dem die Blickrichtung genau senkrecht zur Bewegungsrichtung ist, sind die Lichtlaufzeiten von beiden Stabenden gerade gleich lang und man sieht dieselbe Länge, die man auch misst. In der Bildmitte von Abb. 2 trifft das zu; der Vergleich mit den Karos des Untergrunds zeigt, dass die Maßstäbe gerade entsprechend der Längenkontraktion verkürzt erscheinen.
Kontakt: Möchten Sie uns eine Nachricht senden?